Pascal-þríhyrningur
Pascal-þríhyrningur[1] eða þríhyrningur Pascals[1] er í stærðfræði þríhyrningur af tölum sem raðað er upp eftir kerfi sem Blaise Pascal lýsti, sem nú er þekkt sem einkenni Pascals(en):
- .
Þessi eiginleiki gerir það að verkum að hægt er að raða niðurstöðunum upp á eftirfarandi hátt:

Eiginleikar Pascal þríhyrningsins
Ellefu-veldið
Sjá má mjög fljótlega að fyrstu raðir Pascal-þríhyrningsins stafa út n-ta veldi af 11:
Reglan fellur þó ekki um sig á efri stigum, heldur verður hún bara ekki jafn ljós - , augljóslega, heldur . Þ.e., þar sem að tugir koma fyrir í gildum þríhyrningsins legst tugurinn við næsta sæti fyrir ofan, og einingin verður eftir.
Einkenni Vandermondes
Lát . Þá gildir:
- .
Þessi regla er kennd við Alexandre-Théophile Vandermonde, sem uppgötvaði regluna á átjándu öld.
Tvíliðureglan
Tvíliðureglan notast við stuðla úr Pascal-þríhyrningnum. Til dæmis er , en stuðlarnir (í svigum) passa við 5. línu Pascal þríhyrningsins (fyrsta línan samsvarar ).
Fibbonacci runan
Fibonacciruna kemur fyrir í skálínum Pascal-þríhyrningsins:
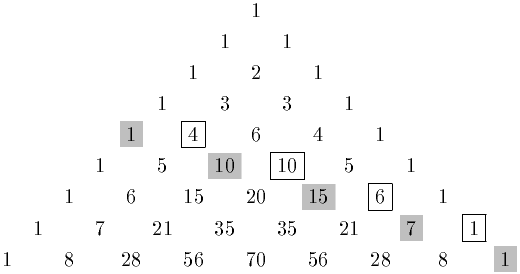
Ef summaðar eru upp gráleitu tölurnar er summan stak í Fibbonacci rununni. Sama gildir um innrömmuðu tölurnar, og hvaða skálínu sem er.
Sönnun á einkenni Pascals
Ímyndum okkur að til sé mengi sem hefur stak. Lát vera stak í og lát . Sjáum að til eru hlutmengi í sem innihalda stök (Sjá: Samantektir). Hinsvegar inniheldur hlutmengi í með stökum ýmist , ásamt öðrum stökum úr , eða það inniheldur stök úr en ekki . Þar sem að það eru hlutmengi af staki úr , þá eru til hlutmengi með stökum úr sem innihalda . Auk þess eru hlutmengi af með stökum sem innhalda ekki , þar sem að það eru hlutmengi af með stökum. Þar af leiðir: