Hjólferill

Hjólferill.

Hjólferill (cýklóða) er sá ferill sem fastur punktur á hring þræðir þegar hringurinn veltur eftir beinni línu án þess að renna til. Þetta er fræg tegund veltiferils þar sem ferillinn er lausn á vandamáli sem Johann Bernoulli setti fram 1696 er nefnist Brachistochrone vandamálið.

Lýsing á ferlinum

Q er miðja hrings, P er punkturinn sem myndar ferilinn og A er skurðpunktur hrings og x-ás.

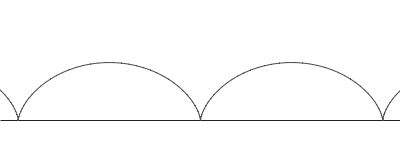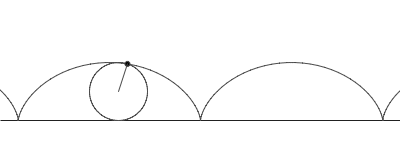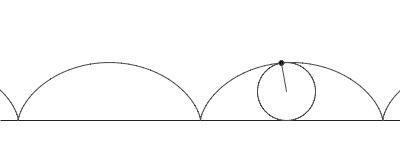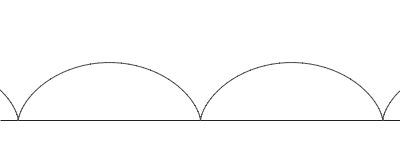
Látum Q vera miðju hjólsins og radíus þess r. Köllum fastan punkt á hjólinu P og látum A vera skurðpunkt hjólsins og línunnar á hverjum tíma. Hornið $\mathrm{\angle }PQA$ köllum við θ. Hjólferill sem hefst í núllpunkti hnitakerfis, þ.e. með P = (0,0) í upphafi, getum við lýst með eftirfarandi stika:

$x=r(\theta -\sin \theta )$

$y=r(1-\cos \theta )$

θr gefur x-hnit miðju hjólsins og er jafnframt fjarlægðin frá A til (0,0).

Ferillinn er diffranlegur alls staðar nema í broddunum þar sem ferillinn snertir línuna (x-ásinn). Þetta má auðveldlega sjá með því að diffra hvora jöfnuna fyrir sig í punktinum (2πr,0), það gefur núll.

Bogamál

Bogamál ferilsins má finna með því að finna lengdina á fyrstu afleiðu vigurfallsins og heilda hana.

$(1){(\genfrac{}{}{0ex}{}{r(\theta -sin\theta )}{r(1-cos\theta )})}^{\prime }=(\genfrac{}{}{0ex}{}{r(1-cos\theta )}{rsin\theta })$

$(2)\Vert (\genfrac{}{}{0ex}{}{r(1-cos\theta )}{rsin\theta })\Vert =\sqrt{(r(1-cos\theta ){)}^2+(rsin\theta {)}^2}=2r|sin(\frac{\theta }{2})|$

$(3)\underset{0}{\overset{2\pi }{\int }}2r|sin(\frac{\theta }{2})|d\theta =4r{[-cos(\frac{\theta }{2})]}_0^{2\pi }=8r$

Þegar hjólið veltur einn hring (2π) fer P eftir hjólferil sem er nákvæmlega 8r að lengd (þar sem r er radíus hjólsins).